ダイクストラ法

はじめに

最短経路を求めるアルゴリズムであるダイクストラ法をPythonで実装して、例題を問いてみます。

追記

例題に ABC 035 D を追加しました。（2018-07-21）

ダイクストラ法

ダイクストラ法は最短経路を効率的に求めるアルゴリズムで、辺の重みが非負のときに使うことができます。詳細は以下の記事を参考にしてください。

• ダイクストラ法 - Wikipedia
• ダイクストラ法（最短経路問題）
• Spaghetti Source - 単一始点最短路 (Dijkstra)

計算量

優先度付きキューを使うことで、O((V+E)logV)で求めることができます*1。

コード

Pythonで優先度付きキューはheapqを用いて実装できます。

from collections import defaultdict
from heapq import heappop, heappush


class Graph(object):
    """
    隣接リストによる有向グラフ
    """

    def __init__(self):
        self.graph = defaultdict(list)

    def __len__(self):
        return len(self.graph)

    def add_edge(self, src, dst, weight=1):
        self.graph[src].append((dst, weight))

    def get_nodes(self):
        return self.graph.keys()


class Dijkstra(object):
    """
    ダイクストラ法（二分ヒープ）による最短経路探索
    計算量: O((E+V)logV)
    """

    def __init__(self, graph, start):
        self.g = graph.graph

        # startノードからの最短距離
        # startノードは0, それ以外は無限大で初期化
        self.dist = defaultdict(lambda: float('inf'))
        self.dist[start] = 0

        # 最短経路での1つ前のノード
        self.prev = defaultdict(lambda: None)

        # startノードをキューに入れる
        self.Q = []
        heappush(self.Q, (self.dist[start], start))

        while self.Q:
            # 優先度（距離）が最小であるキューを取り出す
            dist_u, u = heappop(self.Q)
            if self.dist[u] < dist_u:
                continue
            for v, weight in self.g[u]:
                alt = dist_u + weight
                if self.dist[v] > alt:
                    self.dist[v] = alt
                    self.prev[v] = u
                    heappush(self.Q, (alt, v))

    def shortest_distance(self, goal):
        """
        startノードからgoalノードまでの最短距離
        """
        return self.dist[goal]

    def shortest_path(self, goal):
        """
        startノードからgoalノードまでの最短経路
        """
        path = []
        node = goal
        while node is not None:
            path.append(node)
            node = self.prev[node]
        return path[::-1]

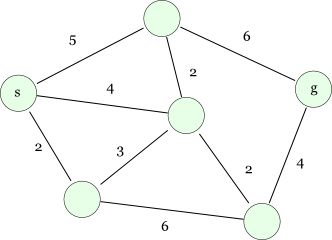
実行例

出典: ダイクストラ法（最短経路問題）

こちらのグラフのノードからノードまでの最短経路を求めてみます。

# (src, dst, weight)
inputs = [(0, 1, 5), (0, 2, 4), (0, 3, 2), (1, 2, 2), (1, 5, 6), (2, 3, 3),
         (2, 4, 2), (3, 4, 6), (4, 5, 4)]

g = Graph()
for src, dst, weight in inputs:
    g.add_edge(src, dst, weight)
    g.add_edge(dst, src, weight)

d = Dijkstra(g, 0)
print('最短経路: {}'.format(d.shortest_path(5)))
print('最短距離: {}'.format(d.shortest_distance(5)))

最短経路: [0, 2, 4, 5]
最短距離: 10

例題

SoundHound Inc. Programming Contest 2018 D - Saving Snuuk

問題

kenkoooo さんはすぬけ国での旅行の計画を立てています。 すぬけ国には 個の都市があり、 本の電車が走っています。 都市には から の番号がつけられていて、 番目の電車は都市 と の間を両方向に走っています。 どの都市からどの都市へも電車を乗り継ぐことで到達できます。

すぬけ国で使える通貨には、円とスヌークの 種類があります。 どの電車の運賃も円とスヌークのどちらの通貨でも支払え、 番目の電車の運賃は、 円で支払う場合 円、 スヌークで払う場合 スヌークです。

両替所のある都市に行くと、 円を スヌークに両替することができます。 ただし、 両替をするときには持っている円すべてをスヌークに両替しなければなりません。 つまり、kenkoooo さんの所持金がX円であるときに両替をすると、 kenkoooo さんの所持金はXスヌークになります。 現在、両替所は 個の都市すべてに存在しますが、 番目の都市の両替所は今年から 年後に閉鎖されてしまい、 年後とそれ以降は使うことができません。

kenkoooo さんは 円を持って都市 から旅に出て、 都市 へ向かおうと思っています。 移動中、kenkoooo さんは両替所のある都市のいずれかで円をスヌークに両替しようと考えています。 ただし、都市 または都市 の両替所で両替をしてもよいものとします。

kenkoooo さんは移動の経路と両替をする都市を適切に選ぶことで、できるだけ多くのスヌークを持っている状態で 都市tに辿り着きたいと考えています。 のそれぞれについて、i年後に都市 から都市 へ移動した際に kenkoooo さんが所持しているスヌークの最大額を求めてください。 ただし、旅行中に年をまたぐことは無いとします。

出典: D - Saving Snuuk

解法

両替を行う都市を として、都市 から都市 までの最小コスト（円）をダイクストラ法で求め、同様に都市 から都市 までの最小コスト（スヌーク）をダイクストラ法で求めます。

n, m, s, t = map(int, input().split())
y = 10**15

yen_g = Graph()
sno_g = Graph()
for _ in range(m):
    u, v, a, b = map(int, input().split())
    yen_g.add_edge(u, v, a)
    yen_g.add_edge(v, u, a)
    sno_g.add_edge(u, v, b)
    sno_g.add_edge(v, u, b)

cost = [0] * n
yen_d = Dijkstra(yen_g, s)
sno_d = Dijkstra(sno_g, t)
for i in range(1, n + 1):
    cost[i - 1] = y - (yen_d.dist[i] + sno_d.dist[i])

ans = [y] * n
ans[n - 1] = cost[n - 1]
for i in range(n - 2, -1, -1):
    ans[i] = max(ans[i + 1], cost[i])

for a in ans:
    print(a)

ABC 035 D - トレジャーハント

問題

高橋君が住む国には 箇所の町と町同士をつなぐ一方通行の道が 本あり、それぞれの町には から の番号が割りふられています。 番目の道は 番の町から 番の町へ移動することが可能であり、移動に 分だけかかります。

所持金が 円の高橋君は 分間のトレジャーハントに出かけることにしました。高橋君は開始 分の時点で 番の町にいます。また、開始から 分の時点にも 番の町にいなくてはなりません。高橋君が 番の町に 分間滞在すると、 円が高橋君の所持金に加算されます。

分間のトレジャーハントによって高橋君の所持金は最大いくらになるか求めてください。

出典: D - トレジャーハント

解法

滞在する町は1つのみで良いので、最短経路で 番から 番の町までに行き、戻ってくることを考えます。 番の町までの往復時間を とすると、所持金は となります。すべての町へ行ったときの所持金を調べて最大値を求めます。

帰り道をからへの経路を考えると、毎回グラフを構築しなくてはならないので、エッジを逆向きに考えて から の経路になるようにします。

N, M, T = map(int, input().split())
A = [int(x) for x in input().split()]

# 行きと帰りの2つのグラフ構築
g1 = Graph()
g2 = Graph()
for _ in range(M):
    a, b, c = map(int, input().split())
    g1.add_edge(a - 1, b - 1, c)
    g2.add_edge(b - 1, a - 1, c)

# ダイクストラ法
d1 = Dijkstra(g1, 0)
d2 = Dijkstra(g2, 0)

# 最短距離を計算
ans = 0
for i in range(N):    
    X = d1.shortest_distance(i) + d2.shortest_distance(i)
    ans = max(ans, A[i] * (T - X))
print(ans)

*1:Vはノード数、Eはエッジ数