kumilog.net

データ分析やプログラミングの話などを書いています。

トップ > 論文メモ > ResNetの論文を読んだ

ResNetの論文を読んだ

論文メモ Deep Learning

ちょくちょくResNetを用いることがあるのですが、論文を読んだことがなかったので、読んでみました。

概要

Residual Network(ResNet)はその名のとおり、残差を用いたネットワークです。ネットワークを深くすると、精度が悪くなるため、それを解決するため、ネットワークを残差関数を学習するよう再構成します。

ImageNetの分類問題のコンペ（ILSVRC 2015）でエラー率3.57%となり、1位を獲得しています。

ResNetが解決する問題

画像分類問題において、ネットワークの層の深さは重要であり、深いほど精度向上すると考えられているが、より深いネットワークを学習させようとすると、下図のように精度が劣化することが知られています。

f:id:xkumiyu:20171104002353p:plain 出典: [1512.03385] Deep Residual Learning for Image Recognition

注目すべきは、training errorにおいても深いネットワーク(56-layer)の方が精度が悪くなっており、過学習が発生しているわけでないということです。

ResNetでは、このような深いネットワークにおいて発生する精度が劣化する問題の解決を目指します。

Residual Learning

ResNetブロック

概要で触れたように、ResNetは残差を用いた学習します。いくつかの積み重ねられた層（ブロック）が、直接最適な写像（変換）になるよう学習するのではなく、残差の写像が最適になるよう学習します。

つまり、入力画像が求める画像*1になるような写像をネットワークが担うのではなく、残差画像になる写像をネットワークが行い、入力画像を足し合わせて求める画像が得られます。

求める写像を \mathcal{H}(x) とすると、入力 x との残差 \mathcal{F}(x): \mathcal{H}(x) - x で表すことができ、元の写像は \mathcal{F}(x) + x となります。 \mathcal{F}(x) + x は以下の図のようにショートカット接続により実現できます。

f:id:xkumiyu:20171104001512p:plain 出典: [1512.03385] Deep Residual Learning for Image Recognition

ショートカット接続はいくつかの層をスキップする単なる恒等写像です。パラメータの追加がなく、計算も複雑にならず、逆誤差伝播も可能なので実装も容易といったメリットがあります。

ResNetブロックの数式での定義は、

$$ y = \mathcal{F}(x, { W_i }) + x \tag{1} $$

となります。 x, y がブロックの入力ベクトル、出力ベクトルであり、 \mathcal{F}(x, { W_i }) は学習すべき残差写像です。上図の場合、ブロックは2つの層からなり、残差写像の関数は \mathcal{F} = W_2 \sigma (W_1 x) で表されます。( \sigma はReLU関数 )

また、 x と F は同じ次元でなければなりません。異なる場合は、

$$ y = \mathcal{F}(x, { W_i }) + W_s x \tag{2} $$

のように、線形射影 W_s を用いて変換することができます。

残差関数 F は柔軟な関数で、ブロックは、2, 3の層（もしくはそれ以上の層）で構成されます。1つの層の場合、ブロックが線形になるため残差が効果的に作用しません。また、ブロックの各層は全結合層でも畳込み層でも用いることができます。

ネットワークアーキテクチャ

ResNetのネットワークは、複数個のResNetブロックで構成されます。下図(の右)の34層ResNetでは、16個のブロックがあります。（1ブロック2層で、最初の畳込み層と最後の全結合層を加え34層です。）

なお、図の真ん中は、比較のためのショートカット接続がないネットワークです（Plain）。

f:id:xkumiyu:20171104002332p:plain
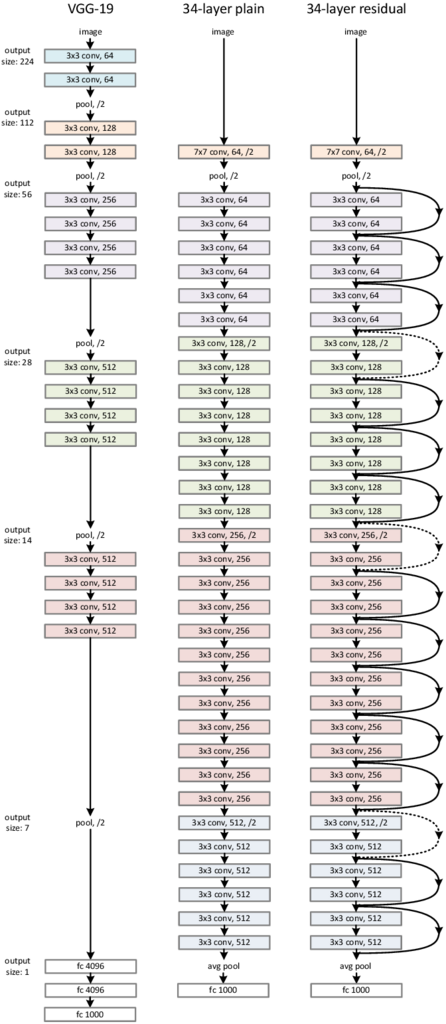
出典: [1512.03385] Deep Residual Learning for Image Recognition

畳込み層はVGGと同じ3x3のフィルタですが、フィルタの数はVGGより少なく、パラメータ数もVGGの18%程度と少なくなっています。

各畳込み層の入力と出力（の特徴マップ）が同じサイズの場合、フィルタの数を同じにし、出力サイズが1/2になる場合、フィルタの数を２倍にします。

式(1)のショートカット接続は、入力と出力が同じサイズの場合に使うことができ、図では実線で示されています。出力のサイズが増加する場合（図の点線）、2つの選択肢があります。

  • (A) 式(1)を使い、増加分をゼロパディングする
  • (B) 式(2)を使う（入力データを変換させる）

パターン(A)を使うと、パラメータは増加しません。

性能評価

評価には、ImageNetのデータ（1000クラス）を用いています。モデルは128万枚の画像で学習され、5万枚の画像で評価しています。

f:id:xkumiyu:20171104002345p:plain 出典: [1512.03385] Deep Residual Learning for Image Recognition

図の左がPlainネットワークで、右がResNetの結果です。また、細い線がTraining Errorで、太い線がValidation Errorです。

Plainネットワークの結果を見ると、18層よりも34層のネットワークの方が、精度が悪いことが分かります。概要で触れた精度の劣化問題が現れています。学習全体を通じて精度が悪いことから勾配消失問題が発生している可能性は低いと思われます。

ResNetは、34層のネットワークは精度が2.8%よくなっており、劣化問題が解決できています。なお、ショートカット接続にはパターン(A)を用いています。

Identity vs. Projection Shortcuts

ショートカット接続には、2パターンあると説明しましたが、性能を比較してみます。

  • (A) 式(1)を使い、ゼロパディングする
  • (B) 次元が増える接続について式(2)を使う（それ以外は式(1)を使う）
  • (C) すべての接続について式(2)を使う
model top-1 err. top-5 err.
plain-34 28.54 10.02
ResNet-34 (A) 25.03 7.76
ResNet-34 (B) 24.52 7.46
ResNet-34 (C) 24.19 7.40

結果は上の表のとおりで、A/B/Cの差はわずかであり、ショートカットの実装方法が劣化問題を解決する本質ではないことを示しています。また、CはAやBより優れていますが、余分なパラメータが増えるため、以降はA/Bを用います。

Deeper Bottleneck Architectures

深いネットワークを構成する場合、ブロックを2層ではなく3層に拡張します。1×1, 3×3, 1×1 の3層にすることで、2層のときの同等の計算コストとなります。

図の左が今までのブロックで、右が3層に拡張したBottlenectブロックです。

f:id:xkumiyu:20171104002336p:plain 出典: [1512.03385] Deep Residual Learning for Image Recognition

Bottlenectブロック使った50, 101, 152層ResNetの精度は以下のとおりです。劣化問題は発生しておらず、深くなるにつれて精度は良くなっています。

model top-1 err. top-5 err.
ResNet-50 22.85 6.71
ResNet-101 21.75 6.05
ResNet-152 21.43 5.71

*1:求める画像は正解画像や教師画像のようなイメージで、ネットワークの出力画像が求める画像に近づけることが学習