Scikit-Optimizeを使ってベイズ最適化で機械学習のハイパーパラメータの探索を行いました。

はじめに

機械学習において、ハイパーパラメータのチューニングは大きな課題の1つです。ハイパーパラメータはSVMでのコストパラメータ $C$ やRBFカーネルの $\gamma$ のことで、人が調整するパラメータのことです。DeepLearningでは、バッチサイズや学習率、層の数、ドロップ率など多岐にわたります。

グリッドサーチ

どのパラメータが良いか探索する方法はいくつかありますが、シンプルな手法の1つにグリッドサーチというものがあります。

グリッドサーチは、用意したパラメータの候補の組み合わせをすべての試す方法です。パラメータが2つあり、それぞれ候補が10個あるならば、試行回数は100回にもなります。

ランダムにパラメータを選択するランダムサーチという手法もあります。違いのイメージは以下の図ですが、詳細はこちらの記事がわかりやすいです。グリッドサーチよりも効率的に探索できるそうです。

出典: Random Search for Hyper-Parameter Optimization

手書き文字での実験

グリッドサーチを手書き文字のデータとSVMでの学習で試してみました。

手書き文字のデータは、scikit-learnで簡単にロードできます。

from sklearn import datasets
digits = datasets.load_digits()

f:id:xkumiyu:20180417215609p:plain

SVMのハイパーパラメータであるコストパラメータ $C$ やRBFカーネルの $\gamma$ を変化させて学習します。探索範囲は、 $2^{-15} \leq C \leq 2^{3}$ , $2^{-5} \leq \gamma \leq 2^{15}$ とし、その範囲内で20個程度のパラメータを選んでいます。

scikit-learnには、GridSearchCVというメソッドでグリッドサーチが使えるのですが、シンプルなアルゴリズムなので自分で書いてみました。Cross-Validationは省いています。

import pandas as pd
from sklearn import svm

scores = pd.DataFrame()
for g in np.logspace(-15, 3, 19, base=2):
    for c in np.logspace(-5, 15, 21, base=2):
        clf = svm.SVC(gamma=g, C=c)
        clf.fit(X_train, y_train)
        scores = scores.append(
                {
                    'gamma': g,
                    'C': c,
                    'accuracy': clf.score(X_test, y_test)
                },
                ignore_index=True)

結果を可視化すると、以下の図のようになります。 $\gamma$ の値が $10^{-3}$ ~ $10^{-4}$ あたりだと $C$ の値はあまり関係なさそうです。

f:id:xkumiyu:20180416223255p:plain

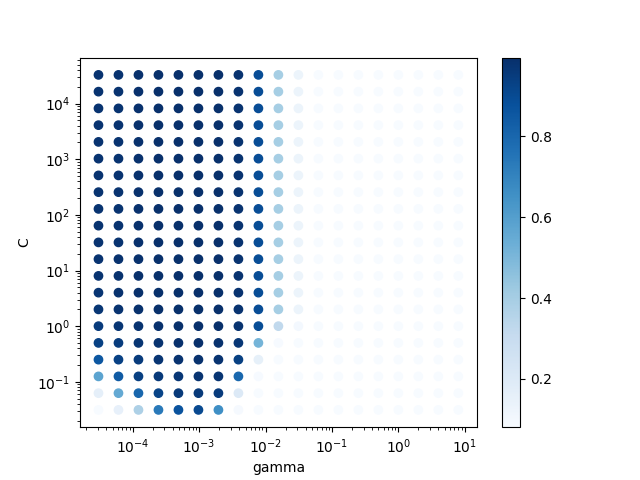
import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel('gamma')
ax.set_ylabel('C')
ax = ax.scatter(scores.gamma, scores.C, c=scores.accuracy, cmap='Blues')
fig.colorbar(ax)
fig.savefig('out.png')

ベイズ最適化

先程のグリッドサーチの例だと、400回近くの施行を繰り返すことになります。そこで、効率的に探索する手法としてベイズ最適化を使ってみます。

ベイズ最適化は、入力 $x$ と出力 $y$ の関係をブラックボックス関数 $f$ とし、この関数をガウス過程に従うとして、出力 $y$ を最大化/最小化する入力 $x$ を探索します。

f:id:xkumiyu:20180418202121p:plain

例えば、以下の関数の最小値を見つける問題を考えてみます。この関数はブラックボックス関数なので、本来ならば中身は全く分かりません。

f:id:xkumiyu:20180419220038p:plain

初期値（赤い点）を与えると、ガウス過程に従う関数(青い線)が予測できます。1点なので、95%信頼区間が広くなっています。

f:id:xkumiyu:20180419223209p:plain

ちなみにガウス過程の予測（回帰）はscikit-learnを用いました。

from sklearn.gaussian_process import GaussianProcessRegressor

gp = GaussianProcessRegressor()
gp.fit(X, y)

評価値に基づき、次に調べる点を決めます。評価値を算出する関数は獲得関数と呼ばれ、PIやEIなどいくつか方法があります。

基本となる考え方は探索と活用です。最小値になると期待できる点（予測関数における期待値が小さい点）を選ぶのが活用で、活用ばかりしていると局所解に陥るので、今まであまり調べていない点（分散が大きい点＝95%信頼区間が広い点）を探索します。

f:id:xkumiyu:20180419223224p:plain

これを繰り返すことによって最小値が効率的に求まります。簡単な例だったので、3点目でほぼ最小値の点を見つけることができました。

f:id:xkumiyu:20180419223242p:plain

f:id:xkumiyu:20180419223301p:plain

参考

ベイズ最適化の詳しい説明は以下のスライドや動画を参照ください。とても勉強になりました。

機械学習のためのベイズ最適化入門 from hoxo_m

Pythonでベイズ最適化

Pythonでベイズ最適化を行うには、Scikit-Optimize (skopt)やGpyOptなどのライブラリがあります。

この2つ試しましたが、GpyOptはドキュメントが少ないのと、対数スケールでの探索が難しいため、今回はskoptを紹介します。

インストールは、pipで簡単にインストールできます。

$ pip install scikit-optimize

探索範囲

まずはじめに探索するハイパーパラメータの範囲を定義します。

離散値や連続値の場合は(最小値, 最大値)のようにtupleで書き、さらに連続値の場合は、事前分布を指定できます。デフォルトは連続一様分布(uniform)で、その他、対数一様分布(log-uniform)が指定できます。カテゴリの場合は[category1, category2, ...]のようにリストで書きます。

グリッドサーチと同じ範囲で、SVMの $C$ と $\gamma$ の定義します。カーネルも変えながら探索できますが、今回はRBFカーネル固定しました。

spaces = [
    (2**-15, 2**3, 'log-uniform') # gamma,
    (2**-5, 2**15, 'log-uniform') # C,
    # ['linear', 'poly', 'rbf']
]

ブラックボックス関数

ブラックボックス関数の定義は、Pythonの普通の関数を定義するだけです。入力 $x$ を引数として受け取ります。x[0]に $\gamma$ 、x[1]に $C$ が入っています。出力は精度にしています。skoptでは最適化できるのは最小化のみなので、最大化したいときは−を掛けます。

def f(x):
    clf = svm.SVC(gamma=x[0], C=x[1])
    clf.fit(X_train, y_train)
    return -1 * clf.score(X_test, y_test)

ガウス過程での最適化

最適化にはgp_minimizeメソッドを使います。獲得関数にEIを使い、試行回数を30回としています。

from skopt import gp_minimize
res = gp_minimize(
    f, spaces,
    acq_func="EI",
    n_calls=30)

結果

結果をグリッドサーチと同じように可視化したものです。

f:id:xkumiyu:20180416223303p:plain

plot_convergenceメソッドを使うと、最小値への収束の様子を可視化できます。

from skopt.plots import plot_convergence
plot_convergence(res, ax=ax)

f:id:xkumiyu:20180416223309p:plain

グリッドサーチでは400回に近い試行回数を行いましたが、このグラフを見ると3回目くらいには最小値に到達しています。

まとめ

ベイズ最適化をScikit-Optimizeを使って行い、SVMのパラメータ探索を行いました。簡単な問題だったのでうまくいきましたが、DeepLearningのような複雑な問題やhyperoptなどの他のライブラリも今後試してみたいと思います。

また、今回使ったコードは以下にまとめてあります。

github.com

kumilog.net

データ分析やプログラミングの話などを書いています。

ベイズ最適化でパラメータチューニングを行う