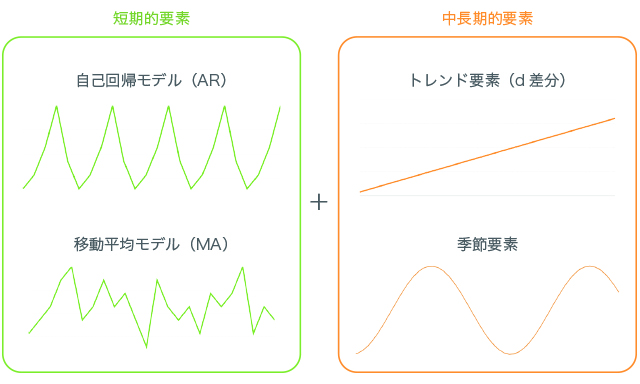
統計モデルでの時系列データの分析手法であるSARIMAを使って、PV数の予測分析を行います。
はじめに
通常、分析で用いるデータは同一の確率分布から得られ、互いに独立である*1ことが前提となっていますが、時系列データは、時間的に互いが関連するデータです。
時系列データはビジネスにおいてもよく見られるデータであり、様々な分析手法があります。そこで、時系列分析手法の一つであるSARIMAを用いて、本サイトのPV数の予測分析を行いたいと思います。
また、今回の分析で使ったnotebookはこちらにあります。
データの準備
データは、Google AnalyticsからエクスポートしたCSVを使います。2017年10月から2018年4月までの7ヵ月間です。
df = pd.read_csv(
'Analytics すべてのウェブサイトのデータ ユーザー サマリー 20171001-20180430.csv', header=5)
df = df.dropna()
df = df.rename(columns={'日の指標': 'date', 'ページビュー数': 'pv'})
df.date = pd.to_datetime(df.date)
df = df.set_index('date')
df = df.reindex(pd.date_range('2017-10-01', end='2018-04-30', freq='D'))
df.pv = df.pv.apply(lambda x: int(x.replace(',', '')))
df.pv = df.pv.astype(np.float64)
予測に使う値はfloat64に変換しておきます。intだとモデルの推定時にエラーが発生しました。
日付をindexにします。date_rangeでfreqを指定して明示的に作った方が良いです。indexを変換する前はエラーが発生してつまりました。恐らくindexが重複していたのが原因っぽいですが。。
データの確認
はじめにデータを確認してみます。いつもmatplotlibだと味気ないので、今回の可視化は主にplotlyを使ってみました。画像にして貼り付けているので動きませんが、本来はマウスオーバーで値が見れたりぐりぐり動きます。動いている感じは、notebookを参照ください。
PV数
print(df.pv.head()) # Output 2017-10-01 2.0 2017-10-02 9.0 2017-10-03 3.0 2017-10-04 21.0 2017-10-05 13.0 Freq: D, Name: pv, dtype: float64
グラフにしてみます。
from plotly import tools from plotly.graph_objs import Scatter, Figure, Layout from plotly.offline import iplot data = [Scatter(x=df.index, y=df.pv, name='pv')] fig = Figure(data=data, layout=Layout(title='PV数')) iplot(fig)

全体的に上昇傾向です。この図だけだと分かりにくいですが、平日のPV数は多く休日は少ないといった特徴を持っています。実際、2倍以上開きがあります。
3月後半の外れ値は、以下の記事がホットエントリーに入ったときのものです。普段は検索からの流入が90%を超えているので、データとして区別できれば面白いかもしれません。
PV / エントリ数
今回の予測に用いませんでしたが、エントリの数が多ければ多いほどほど全体のPV数が増えるのは当然なので、1エントリあたりのPV数も見てみました。ちなみに、このデータの期間内でエントリ数は8から36と4倍以上になっています。

ほとんど同じ傾向で上昇傾向になっています。積み重ねがSEO対策になっているのでしょうか。
相関関係
時系列データは時間的に関連あるデータなので、この関連性について調べてみます。
時間のときのデータを横軸に、1つずらした時間
のときのデータを縦軸にした散布図を描きます。また、ずらす度合いのことをラグといいます。
data = [Scatter(x=df.pv[:-1], y=df.pv[1:], mode='markers')] corr = np.corrcoef(df.pv[:-1], df.pv[1:])[0][1] fig = Figure(data=data, layout=Layout(title='ラグ1の散布図(corr={:.2})'.format(corr))) iplot(fig)

自己相関係数は0.81と、強い相関があることが分かります。つまり前日のデータの影響をかなり受けているといえます。
コレログラム
次にラグ1だけでなく、ラグ2や3の自己相関係数も調べてみます。複数の自己相関係数をプロットしたグラフをコレログラムといい、周期性の確認などに用いられます。
コレログラムはPythonの統計ライブラリであるstatsmodelsのplot_acfやplot_pacfを使うと簡単に描けます。statsmodelsは今回メインで用いるライブラリでこの後も頻繁にでてきます。
import statsmodels.api as sm fig, (ax1, ax2) = plt.subplots(nrows=2, sharex=True) sm.graphics.tsa.plot_acf(df.pv, lags=40, ax=ax1) sm.graphics.tsa.plot_pacf(df.pv, lags=40, ax=ax2)
lagsは用いるラグで、intか配列指定できます。指定しない場合、全データになります。alphaを指定すれば、信頼区間の幅を変えることができます。デフォルトは0.05で95%信頼区間です。

上図(plot_acf)が自己相関で、下図(plot_pacf)が偏相関です。薄い青のエリアは95%信頼区間です。
少し分かりにくいですが、7日間の周期性を持っているようです。平日のPV数は多く休日は少ないといった特徴と一致しています。
成分分解
周期性(季節性)を持っていることが分かったので、季節性の成分を抽出してみます。抽出には、seasonal_decomposeを使います。
from plotly import tools res = sm.tsa.seasonal_decompose(df.pv, freq=7) fig = tools.make_subplots(rows=4, cols=1) fig.append_trace(Scatter(x=res.observed.index, y=res.observed, name='Original'), 1, 1) fig.append_trace(Scatter(x=res.trend.index, y=res.trend, name='Trend'), 2, 1) fig.append_trace(Scatter(x=res.seasonal.index, y=res.seasonal, name='Seasonal'), 3, 1) fig.append_trace(Scatter(x=res.resid.index, y=res.resid, name='Resid'), 4, 1) fig['layout'].update(title='成分分解') iplot(fig)
freqには周期を入力します。戻り値は元データ, トレンド成分, 季節成分, 残差が含まれているオブジェクトです。
ちなみにplotlyを使わなければ、res.plot()一発で図が出力できます。
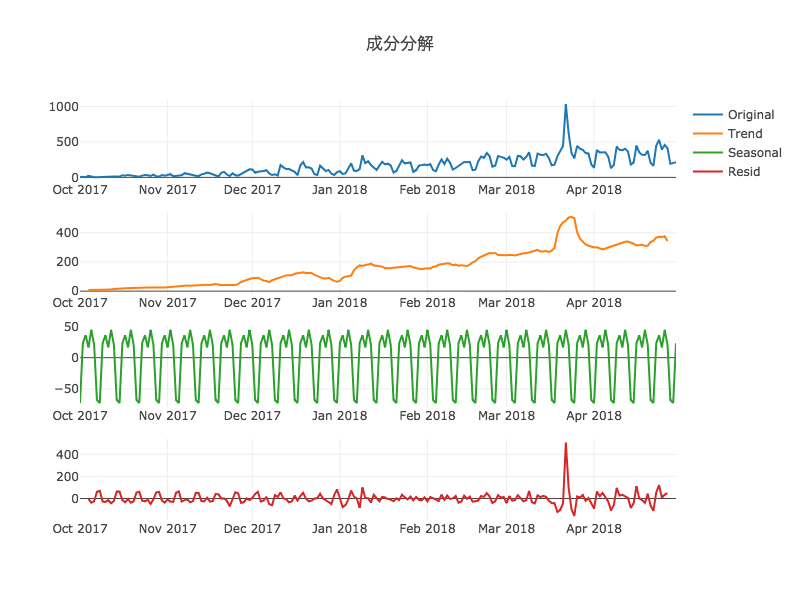
トレンド成分を見ると、元データと比べ滑らかになっており、基本的に単調増加であることがはっきりと分かります。
季節成分を見ると、平日が正で土日が負になっています。また、同じ平日でも水曜と金曜が少し低いのは、ノー残業デーとかであんまり仕事しないからとかですかね。
定常性の確認
ほとんどの時系列分析の手法では、データが定常性(平均と分散が一定)であることを前提にしています。なので、データが定常性か否かを調べます。
定常性は拡張Dickey-Fuller検定(ADF検定)で調べることができ、adfullerを使います。定常性やADF検定について、詳しいことはこちらの記事が参考になります。
res = sm.tsa.stattools.adfuller(df.pv) print('p-value = {:.4}'.format(res[1])) # Output p-value = 0.746
となり、有意水準5%で帰無仮説(定常性を持つ)が棄却されず、このデータは定常性を持つとはいえません。
時系列データの前処理
生データのままだと定常性を持たないので、いくつか処理を行い、定常性を持つデータに変換します。
差分
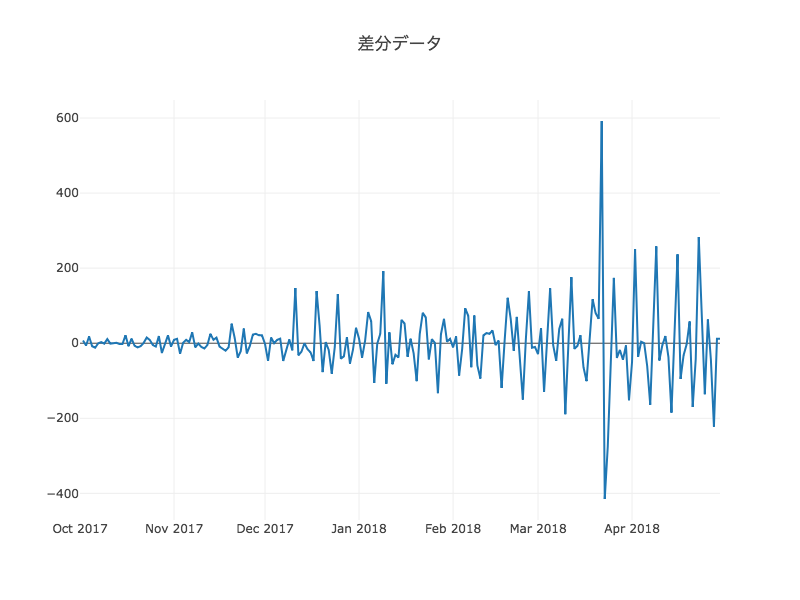
定常性持つデータに変換する方法の1つとして、1時点先のデータとの差分(1階差分)をとります。対数差分をとることもありますが、今回は普通での差分で十分そうです。
data = [Scatter(x=df.index, y=df.pv.diff())]
fig = Figure(data=data, layout=Layout(title='差分データ'))
iplot(fig)
差分は、pandasの場合diffメソッドを使うのが便利です。periodsを指定すれば差分の幅を変えることもできます。
季節調整
季節性を持つデータは、季節成分を取り除き分析しやすい形に変換します。この変換のことを季節調整といいます。
data = [Scatter(x=df.index, y=df.pv-res.seasonal)]
fig = Figure(data=data, layout=Layout(title='季節調整済みデータ'))
iplot(fig)

差分+季節調整
差分と季節調整、この2つの処理を行うと以下のようなデータが得られます。

このデータの定常性を確認します。
seasonal_diff = (df.pv-res.seasonal).diff().dropna() res = sm.tsa.stattools.adfuller(seasonal_diff) print('p-value = {:.4}'.format(res[1])) # Output p-value = 3.963e-10
(どころかほぼ0)となり、有意水準5%で帰無仮説は棄却され定常性を持つを判断できます。
時系列データの予測
それでは、データのモデリングと予測を行っていきます。時系列分析の手法はいくつかありますが、今回は季節性をもつデータなのでSARIMAモデルを使いたいと思います。
SARIMA
SARIMAモデルは以下のように、複数の統計モデルの複合したようなモデルです。それぞれ詳しく知りたい方は、こちらの本を読むと良いと思います。
また、SARIMAモデルは短期的な特徴と中長期的な特徴を表現することができるといえます。
学習データとテストデータ
モデルを推定する前に、学習データとテストデータを用意しておきます。時系列データの場合、時間的に関連があるのでランダムに80%と20%に分けるのではなく、時間で区切って分けます。
2017年10月~2018年3月の6ヵ月間を学習データ、2018年4月の1ヵ月間をテストデータとしました。
train = df[df.index < '2018-04-01'].pv test = df[df.index >= '2018-04-01'].pv
このデータは前処理済みのデータではなく、元データであることに注意します。
モデルの推定
モデルの推定にもstatsmodelsを使います。SARIMAXというメソッドが用意されています。scikit-learnのようにモデルを定義してfitで推定ができます。
from statsmodels.tsa.statespace.sarimax import SARIMAX model = SARIMAX( train, order=(p, d, q), seasonal_order=(sa, sd, sq, s), enforce_stationarity=False, enforce_invertibility=False) result = model.fit()
order=(p, d, q)はARIMAモデルのパラメータで、それぞれ、AR、階差、MAのパラメータです。例えば(1, 0, 0)の場合、AR(1)モデルを表します。
seasonal_order=(sp, sd, sq, s)は季節性のパラメータで、sが周期になります。今回は7日間の周期なのでs=7にします。
ACFとPACFよりパラメータ候補を選定
ARMAのパラメータ(p, q)を自己相関係数(ACF)と偏自己相関係数(PACF)をもとに決める方法があります*2。ACFとPACFからコレログラムを描きましたが、同様にして季節調整済みの差分データのコレログラムを描きます。

ACFの95%信頼区間より外側の点がqの候補になり、同様にPACFよりpの候補を選ぶことができます。少し微妙ですが、qの候補を[0, 7]の範囲、pの候補を[0, 5]の範囲とします。
次に、arma_order_select_icを使い、候補から当てはまりの良いモデルのパラメータを選びます。AICやBICなどの基準をもとにパラメータを選んでいます。
data = seasonal_diff[seasonal_diff.index < '2018-04-01'] res = sm.tsa.arma_order_select_ic(data, max_ar=5, max_ma=7, ic='aic') print(res.aic_min_order) # Output (2, 6)
このメソッドはARMA用のパラメータ探索なので、季節調整済みの差分データを使う必要があります。seasonal_diffが季節調整済みの差分で、その学習データの範囲を入力としています。
結果は、p=2, q=6が良いということらしいです。それ以外のパラメータは決め打ちでモデル推定をします。
model = SARIMAX(
train,
order=(2, 1, 6),
seasonal_order=(1, 1, 1, 7),
enforce_stationarity=False,
enforce_invertibility=False)
result = model.fit()
SARIMAXの入力のtrainは元データになります。差分や季節のパラメータを与えているので、中でいい感じに処理してくれているんだと思います。
予測
推定したモデルを用いた予測はpredictやforcastを使います。
predictは学習データの範囲を含む点の予測を行います。引数に開始時点、終了時点を指定することができますが、指定しない場合は全範囲になります。
forecastは学習データの範囲外の予測を行うものです。引数に予測する点の数を指定します。テストデータ数を入れています。
train_pred = result.predict()
test_pred = result.forecast(len(test))
そのほかにも、get_forecastというのもあり、conf_intで信頼区間が出力できます。
test_pred_ci = result.get_forecast(len(ts_test)).conf_int() print(test_pred_ci) # Output lower pv upper pv 2018-04-01 132.263569 375.789832 2018-04-02 218.869683 495.804919 2018-04-03 290.400642 577.848793 2018-04-04 255.066038 545.121982 2018-04-05 495.299473 787.687981
RMSEで評価
予測したデータのRMSEを算出します。
from sklearn.metrics import mean_squared_error train_rmse = np.sqrt(mean_squared_error(train, train_pred)) test_rmse = np.sqrt(mean_squared_error(test, test_pred)) print('RMSE(train): {:.5}\nRMSE(test): {:.5}'.format(train_rmse, test_rmse)) # Output RMSE(train): 58.447 RMSE(test): 150.03
学習データの誤差はなかなか良いですが、200~500のデータで誤差150というのは結構外れています。
プロット
次に予測したデータをプロットしてみます。plotlyでは信頼区間の色をつけるやり方が難しかったので、matplotlibを使いました。
fig, ax = plt.subplots() df.pv.plot(ax=ax, label='Original', linestyle="dashed") train_pred.plot(ax=ax, label='Predict(train)') test_pred.plot(ax=ax, label='Predict(test)') ax.fill_between( test_pred_ci.index, test_pred_ci.iloc[:, 0], test_pred_ci.iloc[:, 1], color='k', alpha=.2) ax.legend()
青の点線が元データで、オレンジが学習区間の予測、緑がテスト区間の予測です。

見にくいので、テスト区間のみ取り出します。

図で見ても、学習データはよくあてはまっていますが、テストデータは少しずれています。だいたいは95%信頼区間内ですが、いくつか区間外のものもあります。
残差の確認
result.residで残差をみることができます。モデル推定が上手くいっていると、残差はホワイトノイズになるので、残差のコレログラムを描き自己相関がないことを確認します。

問題なさそうです。
自己相関がないことを確認する方法にLjung-Box検定という方法もありますが、今回は明らかに相関がなさそうなので割愛します。
Grid Search
Grid Searchによるパラメータ推定もやってみました。探索したパラメータ数は1,500を超えるので、そこそこ時間(30分くらい?)がかかりました。
p_range = range(0, 6) d_range = range(0, 4) q_range = range(0, 8) sp_range = range(0, 2) sd_range = range(0, 2) sq_range = range(0, 2) history = pd.DataFrame() for p, d, q, sp, sd, sq in itertools.product(p_range, d_range, q_range, sp_range, sd_range, sq_range): if p == 0 and q == 0: continue params = {'p': p, 'd': d, 'q': q, 'sp': sp, 'sd': sd, 'sq': sq} model = SARIMAX( train, order=(params['p'], params['d'], params['q']), seasonal_order=(params['sp'], params['sd'], params['sq'], 7), enforce_stationarity=False, enforce_invertibility=False) result = model.fit(disp=-1) train_pred = result.predict() test_pred = result.forecast(len(test)) score = { 'aic': result.aic, 'bic': result.bic, 'train-rmse': np.sqrt(mean_squared_error(train, train_pred)), 'test-rmse': np.sqrt(mean_squared_error(test, test_pred)) } history = history.append( pd.Series({ **params, **score }), ignore_index=True) print(history.sort_values(by='aic').head()) # Output aic bic d p q sd sp sq test-rmse \ 607 1788.577241 1827.025322 1.0 2.0 7.0 1.0 1.0 1.0 213.233196 859 1788.745876 1827.193957 1.0 3.0 7.0 1.0 0.0 1.0 113.702525 1115 1789.378411 1831.030497 1.0 4.0 7.0 1.0 0.0 1.0 135.805266 1119 1789.942875 1834.798969 1.0 4.0 7.0 1.0 1.0 1.0 157.814221 111 1790.310009 1822.350076 1.0 0.0 7.0 1.0 1.0 1.0 156.144135 train-rmse 607 56.551452 859 56.803243 1115 56.125318 1119 56.008527 111 58.798796
AICが最も良かったパラメータは、order=(2, 1, 7)とほとんど同じで、結果も似たようなものだったので、ここでは割愛します。結果をみたい場合はnotebookをご覧ください。
まとめ
PV数の予測をSARIMAを使って実施しました。汎化性能はまだまだな感じがしますが、意外とよくモデリングできたと思います。
今回は1変数だったので、休日/祝日かどうかやエントリを投稿した日かどうかなどの説明変数を加え、多変数での分析をしたり、状態空間モデルや機械学習系のモデルなどその他の手法での分析を今後やってみたいと思います。
また、今回の分析で使ったnotebookはこちらにあります。
参考
最後に、時系列データの分析にするにあたった読んだ本や参考になったサイトを紹介します。
読んだ本

現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~
- 作者: 横内大介,青木義充
- 出版社/メーカー: 技術評論社
- 発売日: 2014/02/18
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (6件) を見る

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者: 沖本竜義
- 出版社/メーカー: 朝倉書店
- 発売日: 2010/02/01
- メディア: 単行本
- 購入: 4人 クリック: 101回
- この商品を含むブログ (6件) を見る